2025-12-29：判断整除性。用go语言，给定一个正整数 n，先把它每一位上的数字加起来得到 S，再把这些数字相乘得到 P，令 T = S + P。如果 n 能被 T 整除，则返回 true；否则返回 false。
1
输入： n = 99。
输出： true。
解释：
因为 99 可以被其数字和 (9 + 9 = 18) 与数字积 (9 * 9 = 81) 之和 (18 + 81 = 99) 整除，因此输出为 true。
题目来自力扣3622。
步骤一：分解数字
首先，需要获取正整数 n 的每一位数字。代码中使用了一个 for 循环，通过反复将 n 的临时变量 x 除以10并取余数来得到最低位的数字 d。然后，将 x 除以10（向下取整）以移除已经处理过的最低位，直到 x 变为0。这样就能依次得到从低位到高位的每一位数字。
➕✖️ 步骤二：计算和S与积P
在循环分解每一位数字的同时，代码维护两个变量：
• 和 S：初始值为0。每得到一位数字 d，就将其加到 s 上，即 s += d。
• 积 P：初始值为1。每得到一位数字 d，就将其乘到 m 上，即 m *= d。
循环结束后，s 的值就是数字之和 S，m 的值就是数字之积 P。
步骤三：计算T并判断整除性
得到 S和P后，计算T = S + P。最后，判断原始的输入数字n是否能被T整除。在Go语言中，这通过取模运算符%实现。如果n % T的结果等于0，则说明n能被T整除，函数返回true；否则返回false。
⏱️ 空间与时间复杂度分析
• 总的额外空间复杂度：O(1)。在整个计算过程中，只使用了固定数量的额外变量（如 s, m, x, d），这些空间占用不随输入数字 n 的大小而改变。
• 总的时间复杂度：O(d)，其中 d 是数字 n 的位数。因为循环执行的次数等于数字 n 的位数，而每位数字上的操作（取余、加法、乘法）都是常数时间。对于一个正整数 n，其位数 d 约为 log₁₀(n)，因此也可以说时间复杂度是对数级别的 O(log n)。
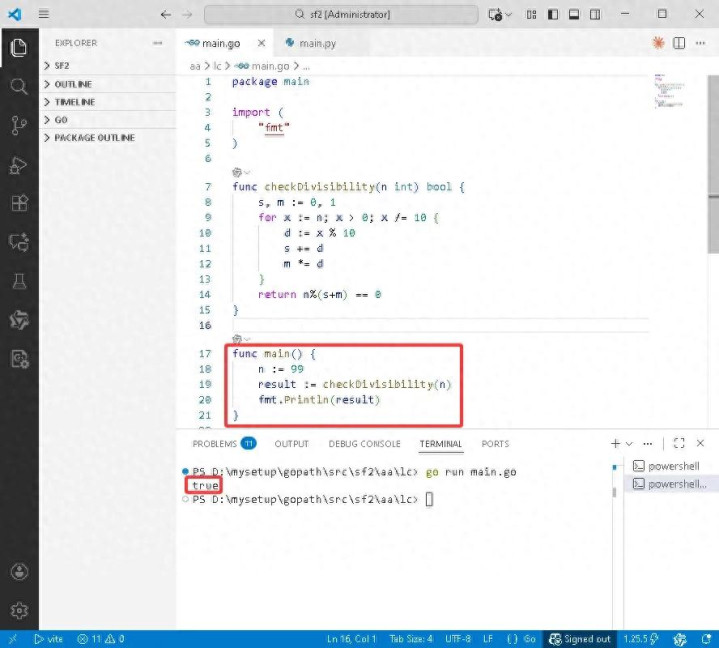
Go完整代码如下：
package main
import (
"fmt"
)
func checkDivisibility(n int)bool {
s, m := 0, 1
for x := n; x > 0; x /= 10 {
d := x % 10
s += d
m *= d
}
return n%(s+m) == 0
}
func main {
n := 99
result := checkDivisibility(n)
fmt.Println(result)
}
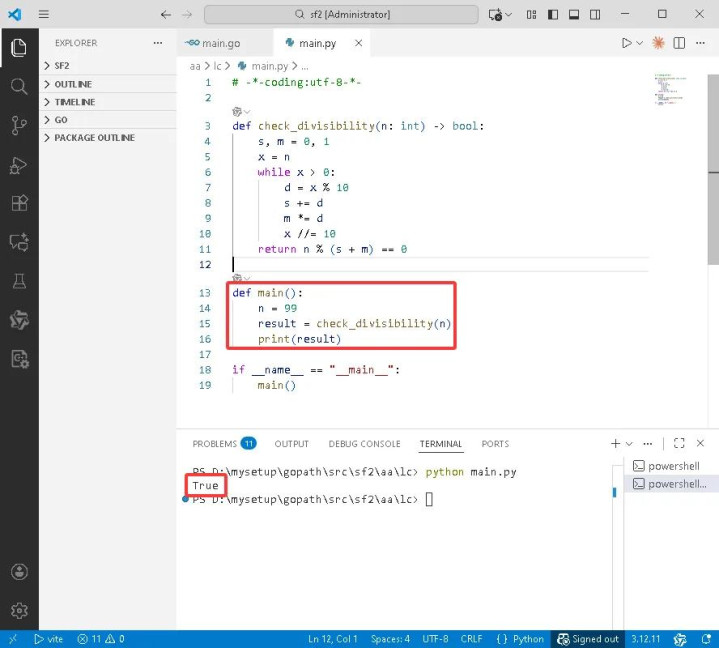
Python完整代码如下：
# -*-coding:utf-8-*-
def check_divisibility(n: int) -> bool:
s, m = 0, 1
x = n
while x > 0:
s += d
m *= d
x //= 10
return n % (s + m) == 0
def main:
n = 99
result = check_divisibility(n)
print(result)
if __name__ == "__main__":
main
C++完整代码如下：
#include
bool checkDivisibility(int n) {
int s = 0, m = 1;
int x = n;
while (x > 0) {
int d = x % 10;
s += d;
m *= d;
x /= 10;
}
return n % (s + m) == 0;
}
int main {
int n = 99;
bool result = checkDivisibility(n);
std::cout
return0;
}
我们相信人工智能为普通人提供了一种“增强工具”，并致力于分享全方位的AI知识。在这里，您可以找到最新的AI科普文章、工具评测、提升效率的秘籍以及行业洞察。
欢迎关注“福大大架构师每日一题”，发消息可获得面试资料，让AI助力您的未来发展。
国内最安全的股票配资平台提示：文章来自网络，不代表本站观点。
- 上一篇：炒股配资公司此案所涉金额是印度政府迄今为止对企业提出的最大索赔
- 下一篇：没有了
